One of the great things about working for Optibus is the ability to apply math to the solution of real world problems. Bus scheduling is a NP-hard problem and as we were developing the Optibus platform in its early days, we encountered many cases that forced us to put our thinking hats on.
One of the problems that illustrates this is what we call “the problem of bringing buses back home.” This was one of our early challenges (I’m glad to say it’s behind us).
The initial problem: vehicle scheduling/assignment
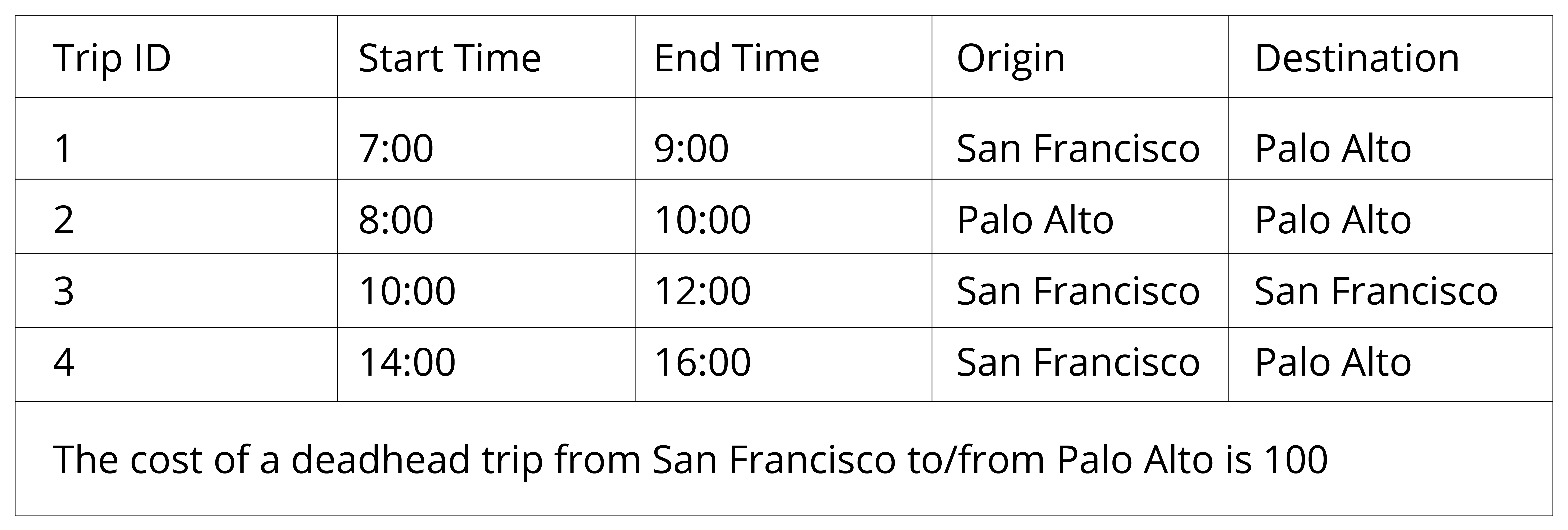
A bus company operates a group of bus routes and gives us some information:
– Where the routes begin and end
– When the buses should run
– Driver-related costs
– Vehicle-related costs
– The maximum number of vehicles available for the delivery of the service
– The allowed driving hours and additional preferences
We input this data into the Optibus platform to produce the output: the vehicle and crew schedule (also known as blocks and runcuts), and the rota (also known as roster). Our commitment – make the schedules work at the lowest cost possible, while applying as many preferences as possible.
Let’s look first at the simpler problem – the vehicle scheduling/assignment problem. With a given amount of routes, we want to allocate the vehicles in the most efficient way and also minimize “deadhead” trips. Deadhead trips mean there is no service or revenue associated with the trip – that’s why we want to minimize them.
Let’s look more closely at the vehicle assignment problem by taking a longer look at an example schedule:
Our goal in this case is to minimize deadhead trips. What we want to do is to ask which trip can come after the other. In this case, trip 2 can’t be performed by the same vehicle as trip 1, since trip 1 isn’t over yet when trip 2 begins. Also, trip 2 can’t happen before trip 3, since they are in a different location without any time left to get from one point to the other. Here’s what we can do:
The best way to represent this problem is a Bipartite Graph.
We want to show as many trip pairs as we can, so we can use as few vehicles as possible, finding the lowest cost option. We do this by looking at Maximum Cardinality.
Maximum cardinality is the maximum number of instances of an entity that can be associated with each instance of another entity.
I can connect 3 with 4, or a pair of 1 with 3 or 4 and 2 with 4. The two arcs we will choose are 1-3 and 3 – 4.
As we have more service trips, the complexity grows and there are some well known algorithmic approaches to help find the best option.
Now let’s look at how we can optimize vehicle scheduling using this approach:
Selecting the maximum cardinality pairs, means that these trips will be performed by the same vehicle, so if we select the 1-3 arc and the 3-4 arc, it means that we will create a vehicle that performs trips 1,3 and 4.
Trip 2 was not selected in any pair, so it will be performed by another vehicle, all alone.
The first trip begins in San Francisco and ends in Palo Alto. Perfect solution? No (at least from the driver’s point of view). This is “the problem of buses going home”.
All Buses Want to Go Home: Single Depot Scheduling
If I were explaining this problem to a kid, I’d say that at night, buses need to go to sleep. Where do they sleep? In depots.
So now we need to insert depots into our graph. To represent depots in the graph, we use a “pull-in” to the depot, a “pull-out” from the depot and add the cost of the pull-out. It looks like this:
We now create a cost to the pull-out because we want to minimize the lengths of depot pull-outs, since they are associated with “deadhead” trips – the drive from the depot to the trip’s origin stop.
All Buses Want to Come Home: Multiple Depot Scheduling
What happens when there is more than one depot? Real-life tends to have more than just one depot for buses.
If I had two vehicles in the depot this is what the options would look like:
In this case, I have two depots: one in San Francisco and one in Palo Alto. The costs for each type of deadhead trip differ. In this case, the Palo Alto pull out is more expensive:
Now things are starting to get really complex… Let’s see why
What If Buses Don’t Go Home? Problem scenarios
Let’s look at a problem scenario:
Here are the options on a graph:
One bus can leave San Francisco, arrive at Palo Alto and stay there, waiting for the next trip, at a deadhead cost of zero. It can also go from Palo Alto to San Jose, at a cost of 50.
The same applies to the bus that begins service in Santa Barbara. It can stay in San Jose for the next trip or go to Palo Alto.
If a bus that originated in San Francisco ends in Santa Barbara, it can stay at the Santa Barbara depot at a cost of zero or travel back to San Francisco at a cost of 350.
This is where the problem starts.
Left alone, the assignment algorithm we just described will leave each bus at the end point – the San Francisco bus will stay in Santa Barbara and vice versa. After all, it’s the cheapest option.
Here is what this problematic scenario would look like:
This is because the algorithms we used so far only look at local considerations. They ignore the fact that the bus began in San Francisco and ended up in Santa Barbara. But buses (or, to be precise, their drivers) want a trip that began in San Francisco to end there. The driver can’t be stranded in Santa Barbara overnight.
The naive solution is a deadhead trip at the end of the day: and in this case we end up with two expensive deadhead trips at the end of the day. The better alternative would be to select a deadhead trip in the middle of the day. This way, we would only pay for the short deadheads between Palo Alto and San Jose, instead of those between San Francisco and Santa Barbara – which are much longer. This is the suggested solution:
Helping Buses Go Home
In order to do this, we need to change how the algorithm works: we need to bring information from the edge of the graph – the fact that the ending depot is Santa Barbara – to the central section in the graph. This means that if the trip ends in Santa Barbara, the algorithm needs to ask whether the original depot pull-out was from Santa Barbara, ensuring the bus comes home at the end of the day.
We need to look at our graph in a different way, and add an extra constraint:
Until now, each arc between trips was neutral towards the depots, but now, we want to mark these arcs as “belonging to” one of the depots: Yellow for San Francisco and Turquoise for Santa Barbara.
The constraint that we add is that for each certain trip, the arc that goes into it is the same color as the arc that comes out of it, connecting it to the next trip.
The arcs between trips can change their “color” according to considerations we will demonstrate later in this post. However, the arcs to and from the depots must always be in the color of that depot.
In our problem, we want to minimize the value of the cost, where the constraint is that the arc color is the same coming into the block and coming out of it. However, solving the problem under this constraint may be computationally unfeasible, so we need to learn how to be able to violate this constraint – adding a penalty for each violation, so we will attempt to avoid it.
Yet, adding these extra constraints to the algorithm isn’t computationally simple. This is actually typical of the many super-interesting problems that we encounter in the mass transit world. How do you schedule at scale and deliver good results when buses need to come home or electric vehicles need to stop and charge? The complexity of electric vehicles itself isn’t simple at all, not to speak of scheduling different types of vehicles, drivers that are compensated in different ways and what happens when depot capacity is also thrown into the mix…
On a personal level, solving these problems is one of the reasons I love working at Optibus – there are endless variations on these problems – and they are challenging enough so that we need to go beyond what’s been used in the industry or even described in academia. And in the end there’s always the pleasure of knowing we helped buses go home.
Read our latest articles:
Relief Vehicle Scheduling
MV transportation – Improving Efficiencies
Bus rapid transit systems planning
Electric vehicle optimization