Gelegentlich hört man von einem berühmten Museumsraub und möglicherweise wundert man sich, wie er gelungen ist. Ich kann nicht erklären, wie sich die Diebe an den ganzen Sicherheitsmaßnahmen in Museen vorbeischleichen könnten, aber ich weiß, wie Diebe darüber entscheiden, was gestohlen werden soll. Und obwohl sich das Planen von Fahrzeugen und Fahrern ziemlich davon unterscheidet, wie ein Raubüberfall auf ein Museum geplant wird, so kann uns die gierige Denkweise eines Straftäters doch einiges über Planoptimierung beibringen.
Stellen Sie sich vor: Sie sind dabei, in ein Museum einzubrechen und haben vor, viele unbezahlbare Artefakte aus seiner Sammlung zu stehlen. Sie verfügen lediglich über ihren Rucksack und weil Sie seit langem nicht im Fitnessstudio gewesen sind, können Sie beim Fliehen nicht mehr als 20 kg tragen. Sie wollen so viele wertvolle Gegenstände mitnehmen, wie möglich, weshalb Sie ausrechnen müssen, wie sich der höchste Gewinn – ohne die 20-kg-Grenze zu überschreiten – abwerfen lässt. Ihre Optionen sind wie folgt:
| Item | Value ($) | Weight (lbs) |
|---|---|---|
| Fossils | 4,340 | 25 |
| Plaque | 330 | 9 |
| Pearl necklace | 1,950 | 7 |
| Marble sculpture | 2,290 | 9 |
| Silver coins | 3,700 | 8 |
| Cash | 3,030 | 4 |
| Block of gold | 4,620 | 11 |
| Museum tickets | 160 | 1 |
| Ancient scroll | 2,780 | 1 |
| Crown | 4,810 | 13 |
Bevor Sie weiter lesen, überlegen Sie sich, wie Sie herausfinden würden, welche Stücke mitzunehmen wären. (Tipp: Sie können die Stücke nach Wert und Kosten/Gewicht sortieren!)
Dieses Szenario ist ein Beispiel des Rucksackproblems, ein einfaches Szenario das durch Optimierung gelöst werden kann.
Sie haben nur wenige Minuten, bevor die Bullen auftauchen, deshalb müssen Sie schnell denken. Sie entscheiden sich dazu, hintereinander die wertvollsten restlichen Artefakte bis zum Erreichen der Gewichtsgrenze in Ihren Rucksack zu stecken.
Sie wählen die Krone, einen Goldbarren, Fossilien und eine antike Schriftrolle aus, zu einen Gesamtwert von 16.550 €. Sie fragen sich, ob Sie diesen Wert übertreffen können, nehmen deshalb alles aus ihrem Rucksack heraus und fangen wieder von Anfang an. Diesmal aber wählen Sie nach den leichtesten Artefakten aus. Nun enthält Ihr Rucksack die Eintrittskarten zum Museum, eine antike Schriftrolle, Bargeld, ein Halsband aus Perlen, Silbermünzen, eine Tafel, eine Skulptur aus Marmor und einen Goldbarren, zu einem Gesamtwert von 18.860 €. Sie erklären sich mit dem höheren Wert zufrieden und verschwinden schnell, bevor Sie erwischt werden.
Greedy-Algorithmus heißt der Mechanismus, den Sie für die Entscheidung, welche Stücke mitzunehmen sind, verwendet haben. Dieser stellt für das Verstehen von Optimierungsvorgängen einen grundlegenden Begriff dar. Hätten Sie tatsächlich den Greedy-Algorithmus nach Wertdichte (Wert ÷ Kosten) verwendet, hätten Sie mit 21.050 € einen noch höheren Gesamtwert erreicht. Weder wäre dies jedoch in jedem Szenario der Fall, noch ist dies der höchstmögliche Wert, den Sie vom Museum hätten stehlen können.
| Greedy Parameter | Algorithm Outcome | Total Value |
|---|---|---|
| Value | Crown, block of gold, fossils, ancient scroll | $16,550 |
| Cost (Weight) | Museum tickets, ancient scroll, cash, pearl necklace, silver coins, plaque, marble sculpture, block of gold | $18,860 |
| Density (Cost/Value) | Ancient scroll, cash, silver coins, block of gold, crown, pearl necklace, museum tickets | $21,050 |
So würde der Code für den Greedy-Algorithmus in Python aussehen:
Das Anwenden des Greedy-Algorithmus bei großen Optimierungsproblemen ergibt ein lokales Maximum, jedoch selten ein globales Maximum.
Es ähnelt der Situation, in welcher Sie den höchsten Berg würden erklimmen wollen, ohne zu sehen, dass ein anderer, entfernter Berg noch höher ist, als der auf dem Sie sich befinden. Um den globalen oder absolut maximalen Wert zu finden, würden wir jedes mögliche Szenario prüfen müssen.
Dies können wir mit einem wie ein Suchbaum funktionierenden, rekursiven Programm tun. Bei jedem Stück, das wir mitnehmen könnten, sehen wir uns den Gesamtwert an, den wir durch die Mitnahme dieses Stückes erlangen würden. Im Vergleich dazu betrachten wir den Gesamtwert, sollten wir dieses Stück nicht mitgenommen haben. Das untenstehende Diagramm stellt mit nur 3 Gegenständen eine vereinfachte Version des Problems dar.
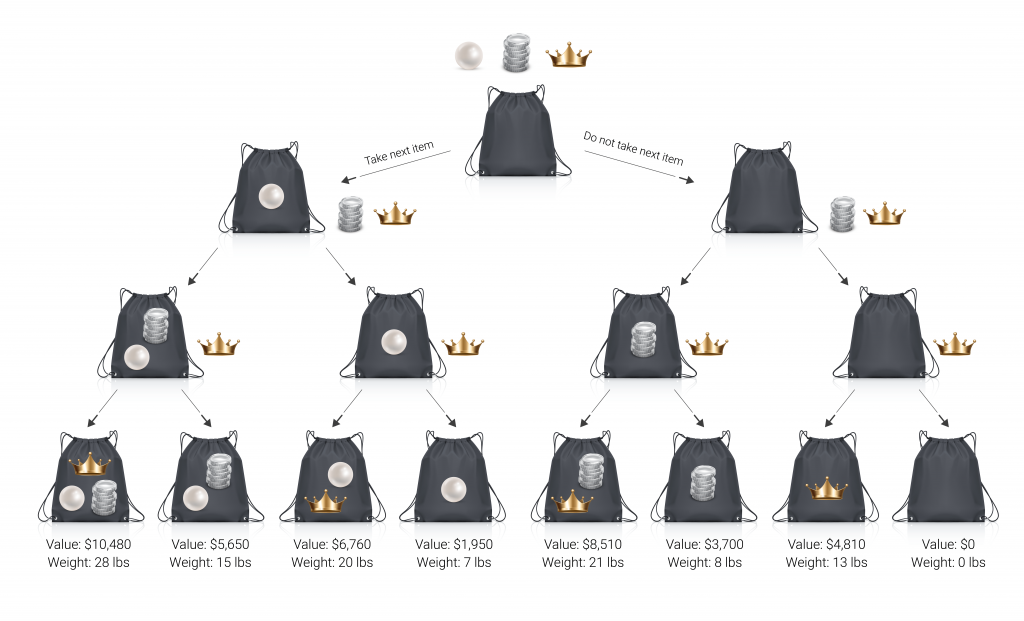
Da wir in diesem vereinfachten Beispiel nur drei Dinge einschließen (die Perlen, das Silber und die Krone), stellen Sie sich 10 kg als Ihre Gewichtsgrenze vor. Welche Dinge würden Sie mitnehmen?
Das Mitnehmen aller drei Dinge wird in diesem Fall offensichtlich den höchsten Gewinn ergeben, aber dabei wird Ihre Gewichtsgrenze überschritten. Der nächstbeste Plan besteht darin, die Krone und die Silbermünze mitzunehmen, denn so wird Ihr Gewinn ohne Überschreitung der 10 kg maximiert.
So würde der Code für diese „Verzweigungs“-Optimierungsmethode aussehen:
Aus diesem Verzweigungsalgorithmus würde sich sogar ein besseres Ergebnis herleiten als das, was der Greedy-Algorithmus ergibt.
Für den Dieb wäre zum Mitnehmen die optimale Auswahl die Krone, die antike Schriftrolle, die Eintrittskarten zum Museum, ein Goldbarren, Bargeld, Silbermünzen und eine Skulptur aus Marmor gewesen, die sich zu einem Gesamtwert von 21.390 € summieren.
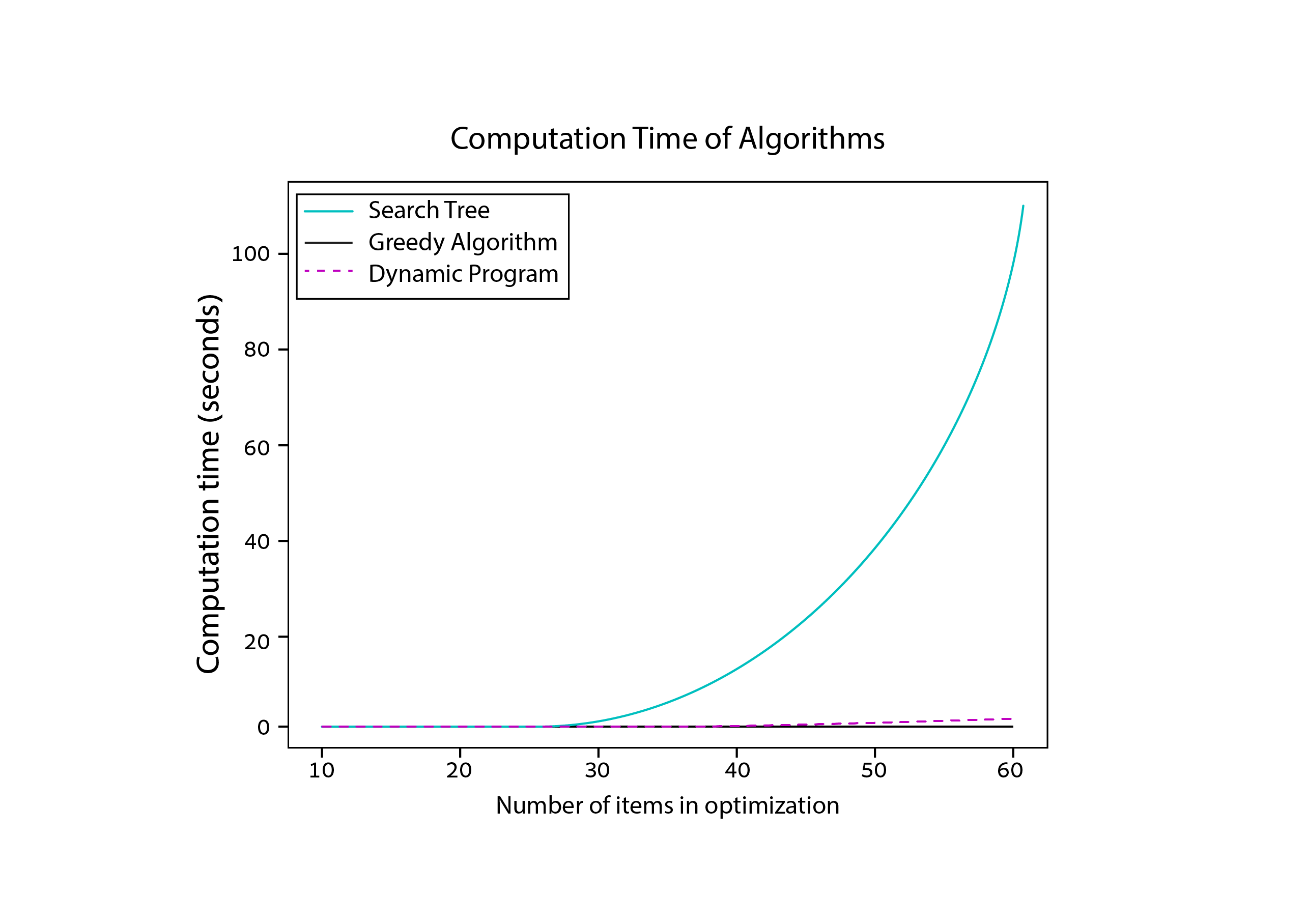
Wie Sie im obenstehenden Diagramm sehen können, wird das Problem wirklich komplex, recht schnell! Das Problem mit 10 Stücken kann ein Computer in weniger als einer Sekunde lösen, wenn es aber 50 Stücke gibt, dauert es einige Sekunden, und mit über 70 Stücken dauert es durchschnittlich mehr als 10 Minuten! Wahre Optimierung ist NP-schwer, das heißt, die Schwierigkeit es zu lösen (mit anderen Worten die dafür benötigte Zeit) nimmt mit steigernder Problemgröße drastisch zu. Im Vergleich bleibt der Greedy-Algorithmus mit einer Dauer von nur wenigen Millisekunden dahingegen stabil. Kein Wunder also, dass ein Einbrecher das Anwenden des Greedy-Algorithmus bevorzugen würde, da er ihm viel Zeit ersparen würde.
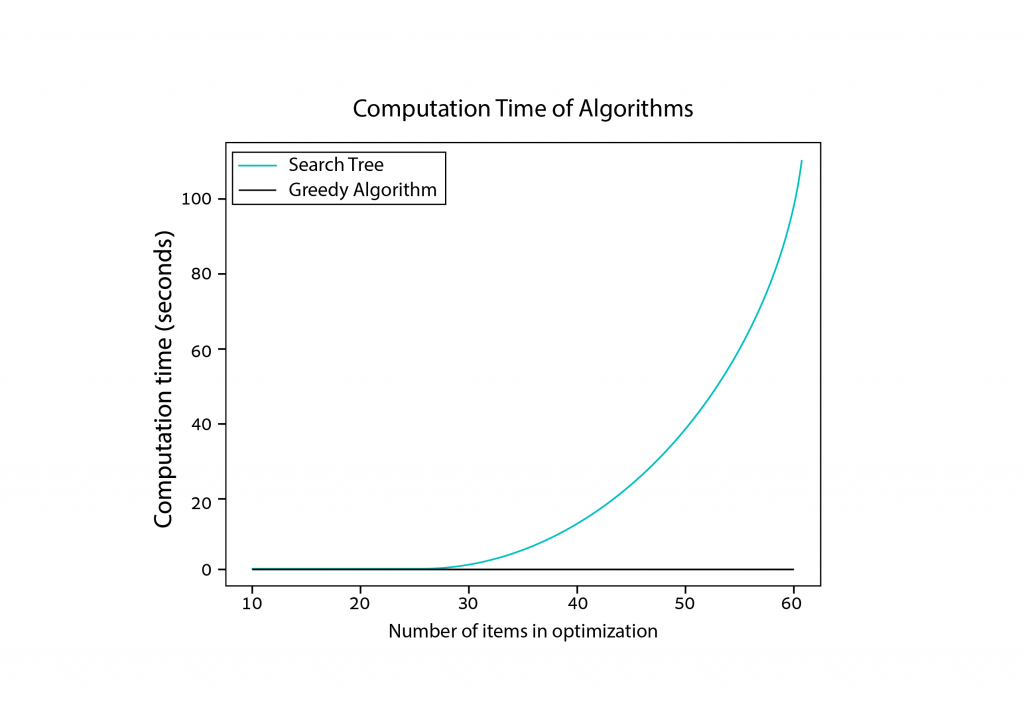
Es gibt aber einen Kompromiss.
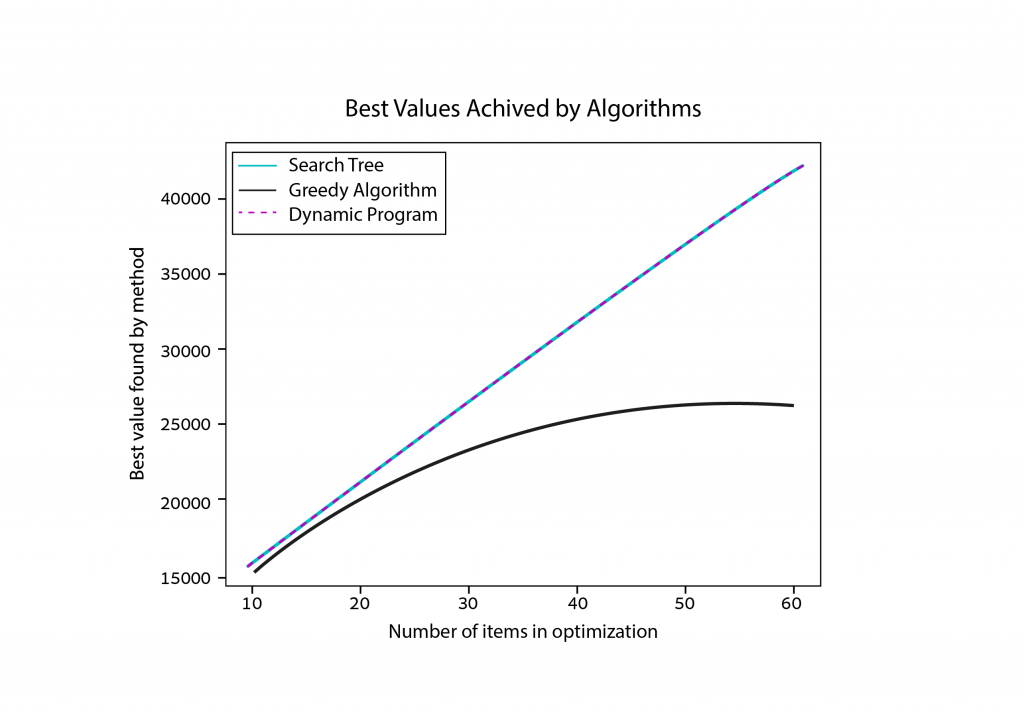
Dass sich aus dem Greedy-Algorithmus nicht immer die beste Lösung ergibt, wussten wir schon. Immerhin kam er ihr im vorigen Beispiel ziemlich nahe. Im folgenden Graph wird sichtbar, dass – wenn die Problemgröße steigt – der durch jedes Verfahren erzielbare Unterschied zwischen den optimalen Werten ebenso zunimmt.
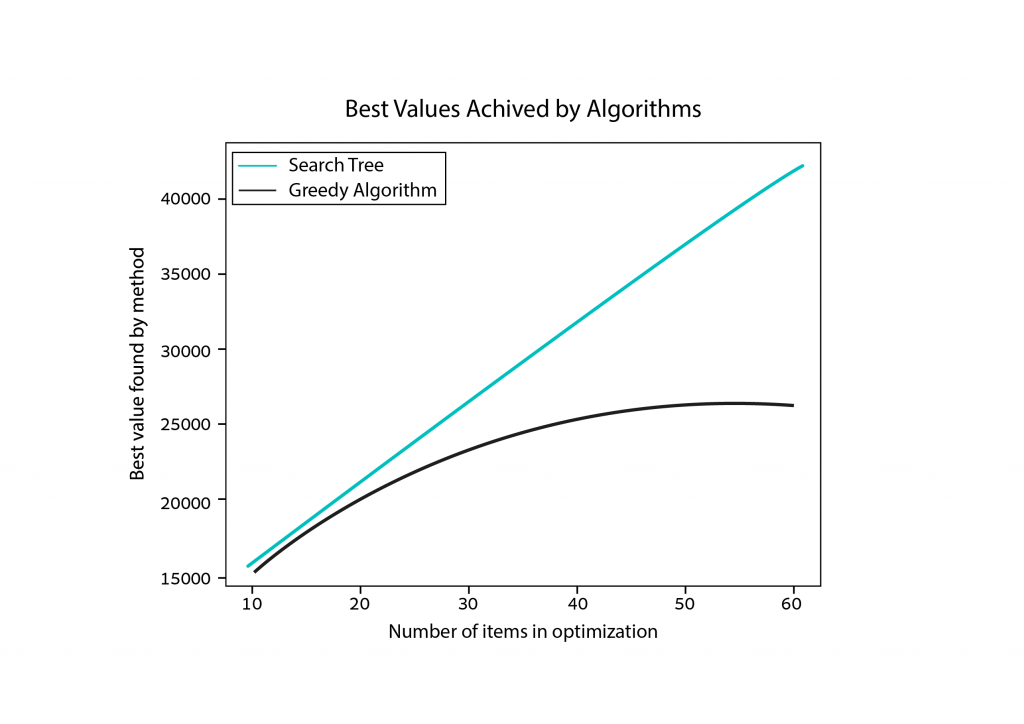
Gibt es eine effizientere Optimierungsstrategie?
Beachten Sie, wie viele der Zweige – oder Teilprobleme – im oben abgebildeten Rucksack-Diagramm einander ähneln. Dynamische Programmierung – eine fortgeschrittene Optimierungsstrategie – spart Rechenleistung, indem Ergebnisse aus diesen Teilproblemen für spätere Anwendung zwischengespeichert werden (durch eine sogenannte Memoization-Technik). Es stellt sich heraus, dass diese Herangehensweise eine Menge Zeit spart! Und da Algorithmen bei der dynamischen Programmierung der Suchbaumstruktur folgen, werden Ergebnisse stets optimal sein. Durch dynamische Programmierung können wir binnen einem dem Greedy-Algorithmus näheren Zeitrahmen optimale Ergebnisse berechnen. Werfen Sie einen Blick auf den nachstehenden Graphen.
Also, was kann uns ein Einbrecher hinsichtlich Planung beibringen?
Irgendwie sind Verkehrsplanungsprobleme dem Rucksackproblem ähnlich. Wenn wir das Verkehrsnetz einer Stadt planen und seinen Betrieb optimieren, wählen wir bedingt durch einen Satz von Einschränkungen Linien und Fahrten für jedes Fahrzeug und jeden Fahrer aus. Dabei ähnelt unsere Herangehensweise der des Einbrechers, wenn er Stücke auswählt, die er aus dem Museum stehlen will.
Das Problem wird jedoch im echten Leben noch viel komplexer. Erstens haben wir viele „Einbrecher“. In gewisser Hinsicht bilden alle Fahrzeuge und Fahrer ein Einbrecherteam und um das beste kombinierte Ergebnis zu bekommen, wollen wir jede einzelne ihrer Operationen optimieren. Zweitens sind reale Einschränkungen viel komplizierter, da wir hierbei mit Menschen und Ungewissheiten arbeiten. Wir könnten zum Beispiel eine Einschränkung haben, nach welcher ein Fahrer mindestens alle 4 Stunden Arbeitszeit eine Pause von 30 Minuten an einem bestimmten Ort braucht. Im echten Leben könnten sich Fahrten auch noch verspäten, daher kann die Berücksichtigung verspäteter Fahrten bei der Planung die Pünktlichkeitsleistung verbessern und Kürzungen vermeiden.
Der Einbrecher will sein Optimierungsproblem so schnell wie möglich lösen und Optibus ebenso – aber wir sind nicht bereit, uns mit der „gierigen“ Lösung zufriedenzustellen.
Diese Verkehrsplanungsprobleme sind wie beim Rucksackproblem NP-schwer und erfordern zur richtigen Lösung ein breites Arsenal von fortgeschrittenen Heuristiken und Algorithmen.
Bei der Lösung großer Umlauf- und Dienstplanungsprobleme müssen wir ein breites Spektrum an Kompromissen und Einschränkungen berücksichtigen, wie zum Beispiel Kosten, Pünktlichkeitsleistung, Arbeitsgesetze und weitere Verordnungen. Um die beste Lösung erreichen zu können, müssen wir zahlreiche unterschiedliche Variablen berücksichtigen und mehrere unterschiedlich mögliche Ergebnisse prüfen.
Bei Optibus benutzen wir für die Lösung dieser Verkehrsoptimierungsprobleme in der Cloud eine Kombination aus Graphentheorie-verwandten Algorithmen, maschinellem Lernen und KI-Algorithmen. So sind wir in der Lage, Probleme in einer verteilten Art zu lösen und bringen dabei massive Cloud-Ressourcen und serverfreie EDV zur Geltung. Dies ermöglicht uns, den Betrieb größerer Verkehrsnetze in sehr kurzer Zeit zu planen – als ob wir lediglich beim Lösen eines einfachen Rucksackproblems wären.